BÀI TOÁN HÌNH THANG TRONG ĐỀ THI BIMC 2018 (Toán học trẻ quốc tế tại Bulgaria)

Nhìn chung các quốc gia trong khu vực châu Á – Thái Bình Dương đề cậpkiến thức hình họcsớm hơn Việt Nam. Định lý Pitago (Pythagoras)được giới thiệu ở các nước từ lớp 5 còn ở Việt Nam từ lớp 7. Vì thế, trong thời gian 4 phút, bài toán hình thuộc đề BIMC 2018 (Toán học trẻ quốc tế tại Bulgaria) dưới đây được đánh giá là khó đối với học sinh khối 6-7 của Việt nam.

Topic 15: Pythagoras’ Theorem

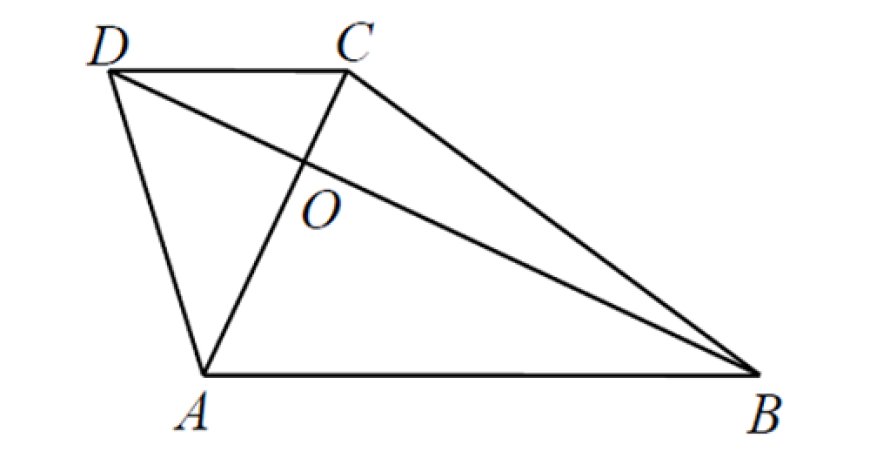
Problem:In quadrilateral ABCD, AB is parallel to CD, and the diagonals AC and BD are perpendicular and intersect at point O. If AO = p cm, CO = q cm, BO = r cm,

DO = s cm, AB = 7 cm and CD = 3cm, what is the value of pq + rs?

Dịch đề:Trong tứ giác ABCD có AB song song với CD, hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại điểm O. Biết AO = p cm, CO = q cm, BO = r cm, DO = s cm, AB = 7 cm and CD = 3cm, tính giá trị của pq + rs.

Solution

Sau đây chúng tôi sẽ trình bày 2 cách giải cho bài toán này:

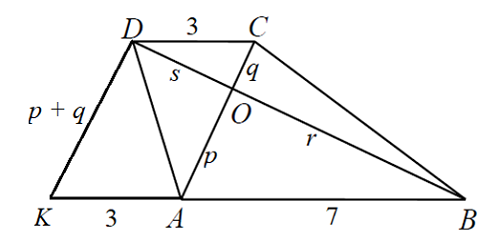
Ký hiệu các độ dài trong hình vẽ và đường phụ DK trong cách 2